Deutsch-Josza 算法
量子算法是量子计算落地实用的最大驱动力,好的量子算法设计将更快速推动量子计算的发展。
Deutsch-Jozsa 量子算法,简称 D-J 算法, David Deutsch 和 Richard Jozsa 早在 1992 年提出了该算法, 这是第一个展示了量子计算和经典计算在解决具体问题时所具有明显差异性的算法。
D-J 算法是这样描述的: 给定两个不同类型的函数,通过计算,判断该函数是属于哪一类型的函数,其可用来演示说明量子计算如何在计算能力上远超经典计算。
D-J 算法所阐述的问题是: 考虑一个函数𝑓(𝑥), 它将 n 个字符串 x 作为输入并返回 0 或 1。注意,n 个字符串也是由 0 和 1 组成,函数形式如 图 4.2.3.1 所示:
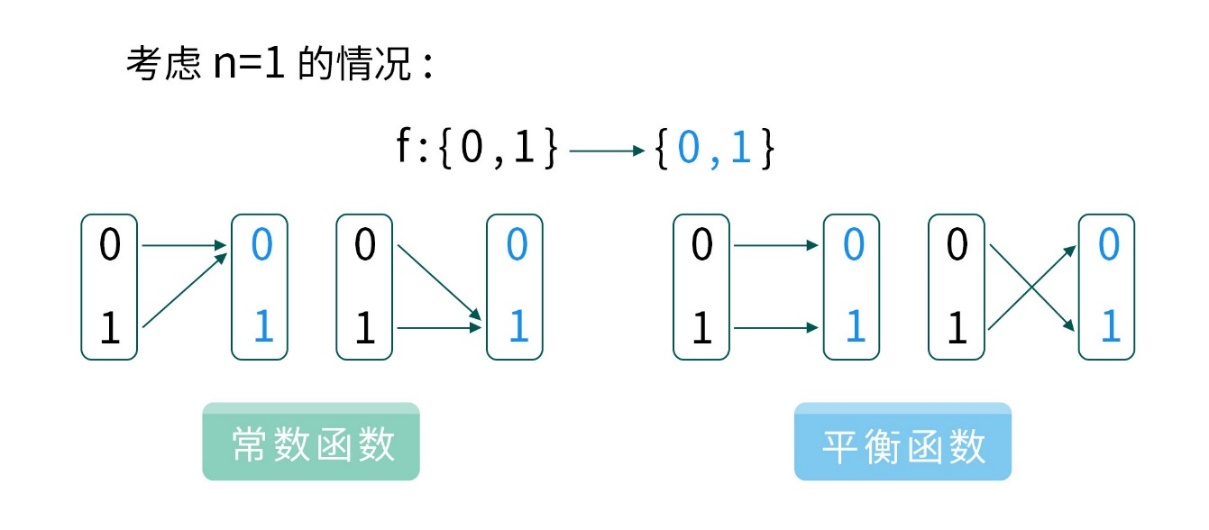
这个函数称为 常数函数。 如果对任意𝑓(𝑥) 都等于 0 或者𝑓(𝑥) 都等于 1:
而如果𝑓(𝑥) = 0 的个数等于𝑓(𝑥) = 1 的个数, 则称这个函数为 平衡函数:
下面考虑一下最简单的情况: 当 n=1 的时候, 常数函数的类型是这样的: 𝑓(0), 𝑓(1)都指向 0; 或者𝑓(0), 𝑓(1)都指向 1, 而平衡函数则是各占一半。 回顾问题,要解决的是: 给定输入和输出,如何快捷地判断 f(x)是属于 常数函数,或是 平衡函数。
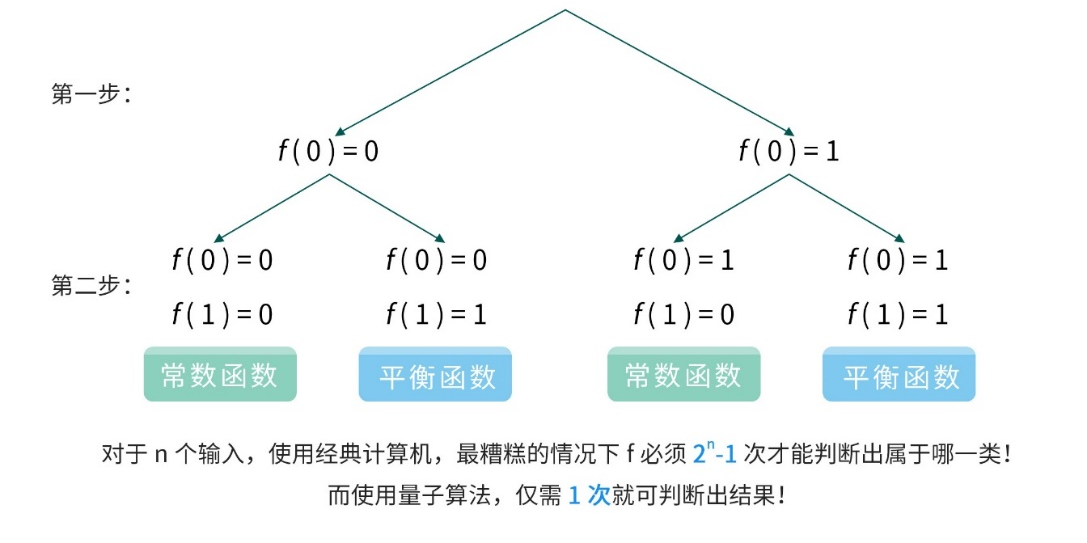
图 4.2.3.2 在经典算法中,给定了输入之后, 第一步是需要判断𝑓(0), F(x)有两种情况, 𝑓(0) = 0 或者𝑓(0) = 1; 当确定𝑓(0)之后,再判断𝑓(1),确定了𝑓(1)的值之后,就可以确定该函数的类型; 整个过程需要两次,才可以判断函数的类型。 按照这样的方式,对于经典算法𝑛个输入, 在最糟糕的情况下 f 必须要2𝑛−1 + 1次才能判断出函数属于哪一类, 即,最糟糕情形需要验证一半多一个数据; 而如果使用量子算法,仅需 1 次就可以判断出结果。
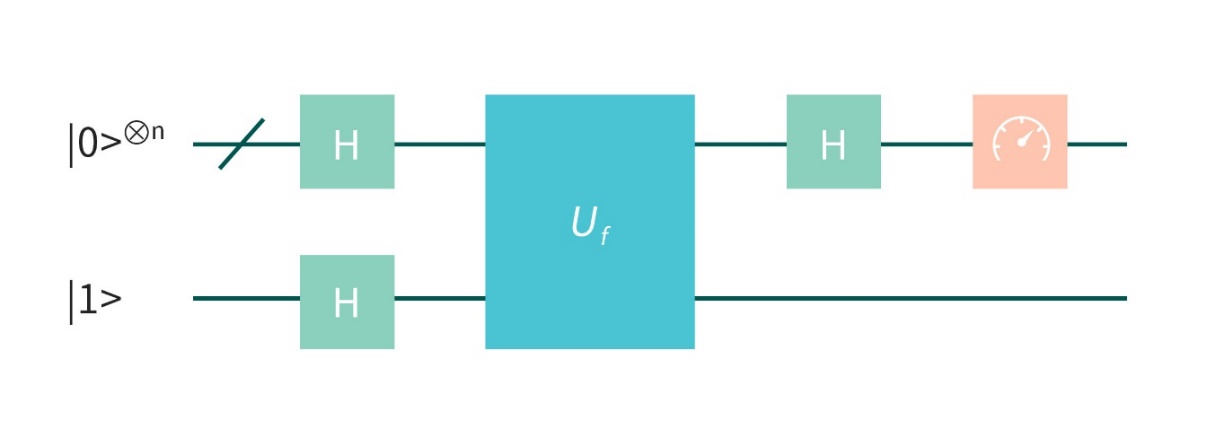
通过 图 4.2.3.3 所示的量子线路图来理解该算法是如何解决问题的。 首先,对所有的比特都执行 Hadamard 门操作,然后经过黑盒子 Uf,再对工作比特添加 Hadamard 门,然后测量。
按照实施步骤,表达形式: 1. 初始化
在本源量子云计算服务平台上实现 D-J 算法
在云平台注册并登陆后,可以看到这样的主界面:
云平台以项目为单位管理多个量子程序的编写和结果。从创建一个新的项目开始,点击屏幕下方的“新增“按钮,会跳出一个引导:
在具有真实量子芯片权限后,这里会出现量子芯片的选项,为了学习只需要通过经典计算机对量子计算机进行仿真,这里使用的是本源 32 位量子虚拟机。点击下一步:
这个界面可以填入新建项目的名称和描述。名字是随意的,项目描述是可选的,这里可以写“DJ-算法学习”。
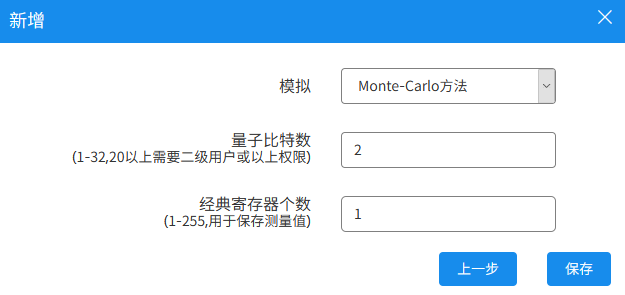
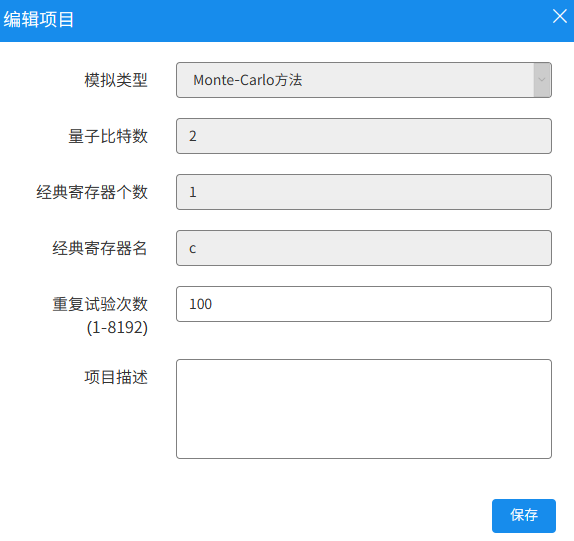
这个界面可以选择量子计算模拟的一些参数。在模拟方法上,可以选择两种: Monte-Carlo 方法和概率方法。 - Monte-Carlo 方法: 通过多次数值模拟,对测量结果进行仿真。 - 概率方法: 直接计算出需要的比特概率分布,而不需要真正的去计算测量过程。
其中概率方法比 Monte-Carlo 方法运行会快一些;由于是多次随机, Monte-Carlo 方法每次运行的结果可能会不一样。这里选择 Monte-Carlo 方法。
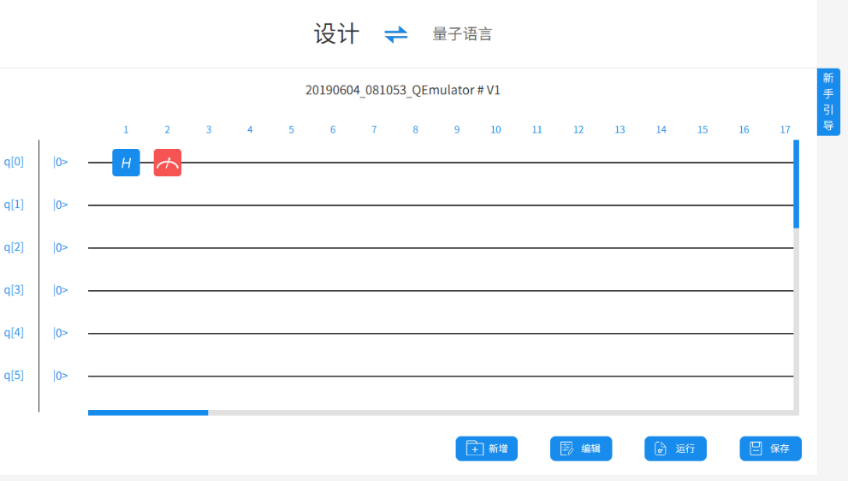
以两个量子比特的 DJ 算法为例,它需要使用 2 个量子比特和 1 个经典寄存器去保存一次测量的值, 输入好之后,点击保存。现在可以看到编程的主界面:
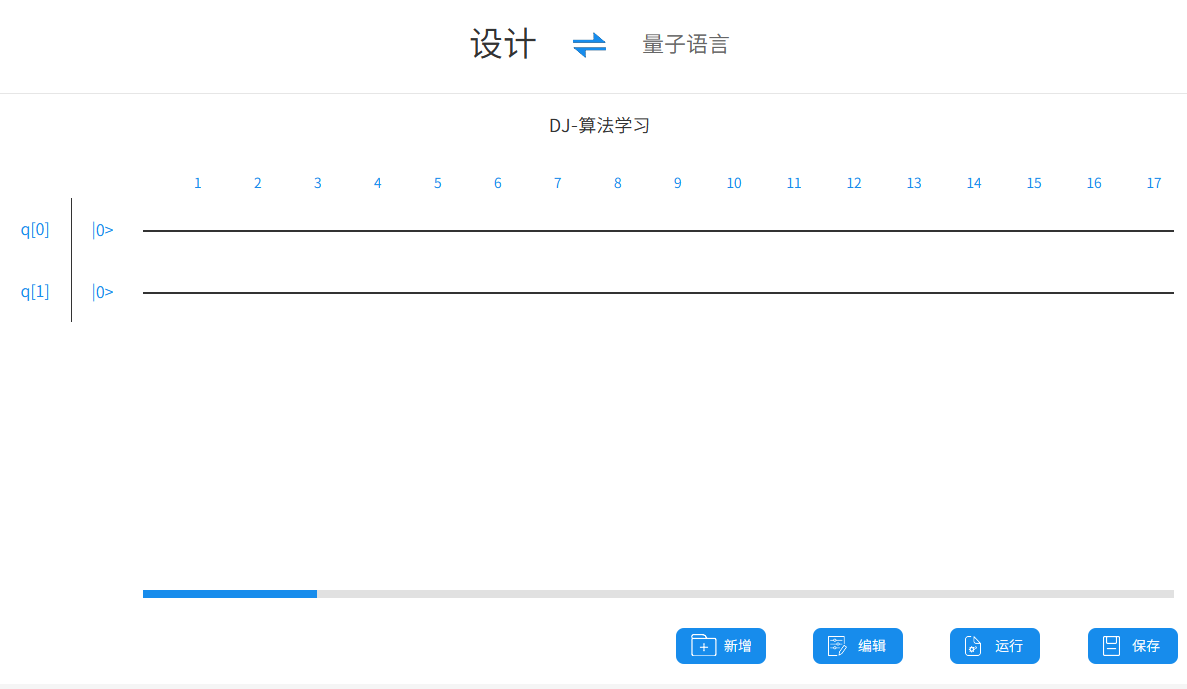
在空白的线上点击,即可在此处添加一个量子逻辑门。根据 DJ 算法的内容,首先需要在第一条线上添加一个 Hadamard 门。

由此,可以看到出现了一个待选量子逻辑门列表。鼠标移动到各个逻辑门的符号上,可以看到逻辑门的解释。点一下 H 就可以在此处插入一个 Hadamard 门。
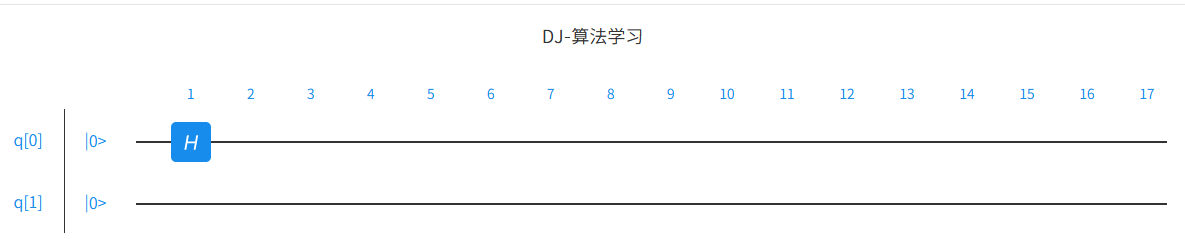
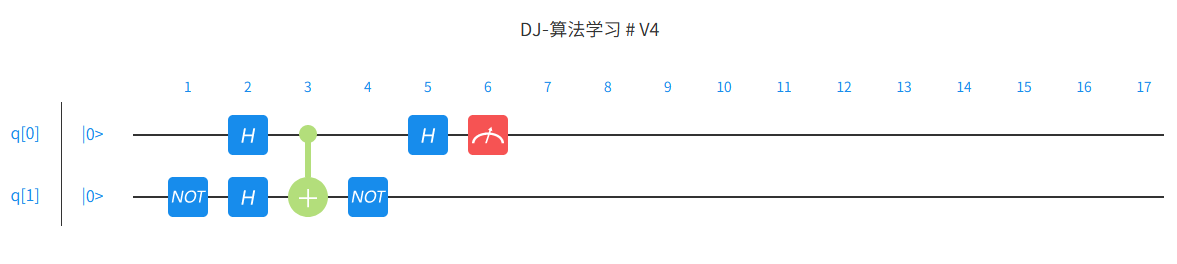
插入逻辑门之后,双击这个逻辑门可以删除,也可以通过鼠标拖动这个门的位置; 同样在其他地方点击,可以插入更多的量子逻辑门。根据 DJ 算法, 将除了 Oracle 的部分添加上:
中间空出来的部分,就是 Oracle 可以插入的部分了。
有很多量子算法, Oracle 是作为输入给出的,比如 DJ 算法和 Grover 算法等。所以,两比特 DJ 算法的量子程序就已经写好了。
这里,可以插入不同的 Oracle 试验一下;定义 Oracle 的输入输出是:
这里 f(x)会根据 Oracle 不同而编码到量子线路中,例如一个 CNOT 门就可以做一个Oracle。
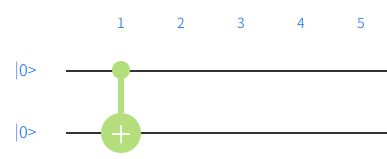
一个 CNOT 门的效果是,
对比上面的 Oracle 公式,相当于 f(x)=x。由此, 可以看出 f(0)=0, f(1)=1,因此是一个平衡函数。
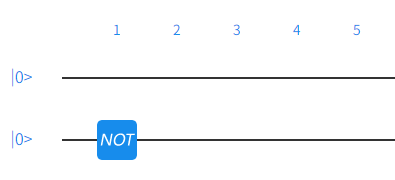
这个门能产生的效果是|x⟩|y⟩ → |𝑥⟩|(1 + 𝑦)mod2⟩,对比上面的 Oracle 公式,相当于f(x)=1,这是一个常数函数。
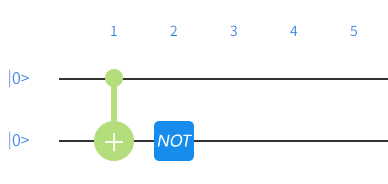
这个相当于把两种情况组合起来了,效果是|x⟩|y⟩ → |𝑥⟩|(𝑥 + 𝑦 + 1)mod2⟩,因此对应了 f(x)=x+1,同理,这是一个平衡函数。
依次来检验这三种 Oracle, DJ 算法是否能输出正确的结果。
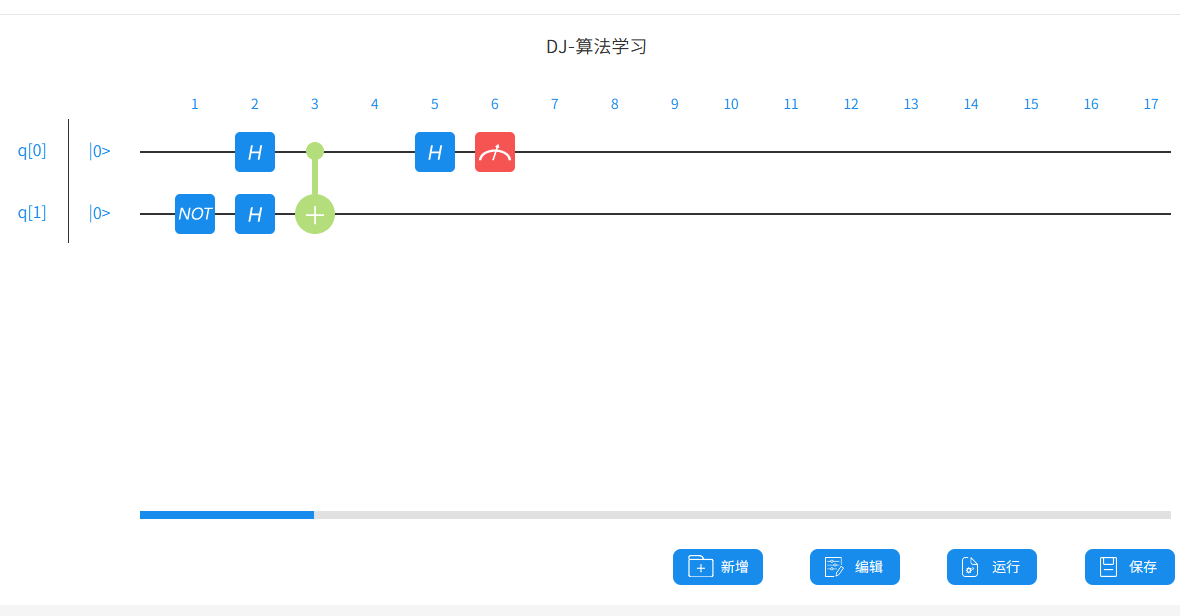
第一种: CNOT
在第一个 Qubit 上得到 100%的 1 测量值, 点击“编辑”, 可以编辑重复测量的次数,默认 100 次;点击运行,就可以开始运行这个量子程序了。
结果显示得出一个图表:
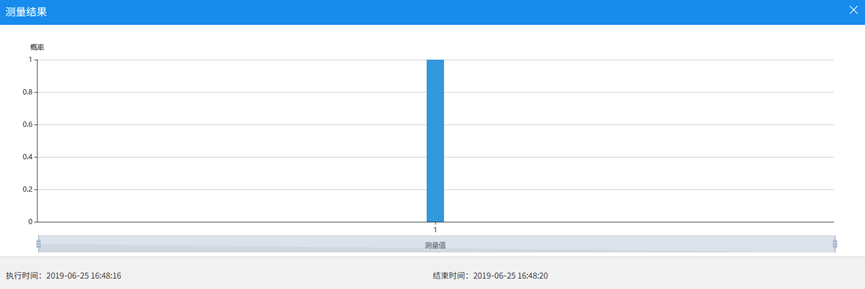
这个柱状图的横轴表示不同的测量值,纵轴表示这个测量值对应的概率。这里只测到了 1,概率为 100%,符合预期。
依次测试另外两种 Oracle:
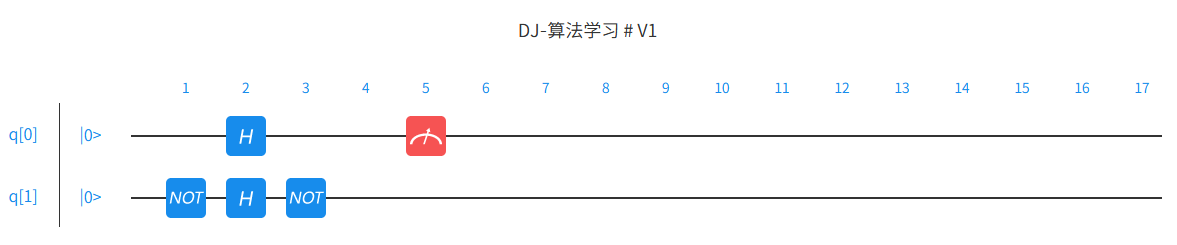
对于这种情况,可以看到测量值 100%为 0。
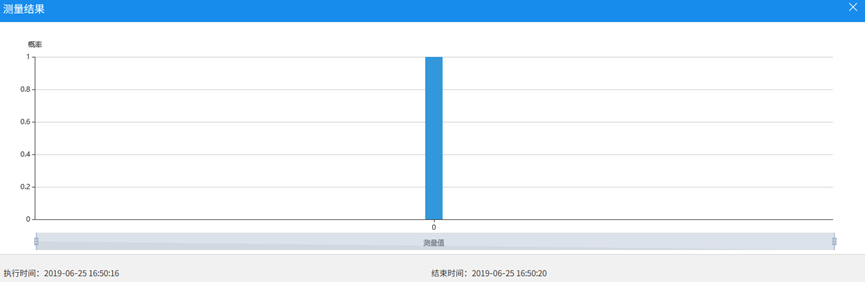
第三种情况:
由此,可以得到 100%的 1,说明这个 Oracle 代表一个平衡函数。
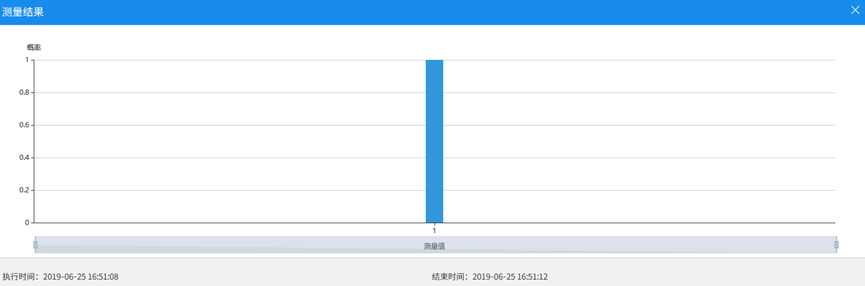
如上述,在云平台上,可以实现简单的两比特量子算法。
在 QPanda 上实现 DJ 算法
下面的代码可以在 github 的 QPanda 仓库中找到。
#include "Utilities/Utilities.h"
#include "Utils/Utilities.h"
#include "QPandaNamespace.h"
#include "Core/QPanda.h"
#include <vector>
using namespace std;
USING_QPANDA
using QGEN = function<QCircuit(Qubit*, Qubit*)>;
QGEN The_Two_Qubit_Oracle(vector<bool> oracle_function) {
return [oracle_function](Qubit* qubit1, Qubit* qubit2) {
QCircuit prog;
if (oracle_function[0] == false && oracle_function[1] == true) {
// f(x) = x;
prog << CNOT(qubit1, qubit2);
} else if (oracle_function[0] == true && oracle_function[1] == false) {
// f(x) = x + 1;
prog << X(qubit2)
<< CNOT(qubit1, qubit2)
<< X(qubit2);
} else if (oracle_function[0] == true && oracle_function[1] == true) {
// f(x) = 1
prog << X(qubit2);
} else {
// f(x) = 0, do nothing
}
return prog;
};
}
QProg Two_Qubit_DJ_With_Oracle(Qubit* qubit1, Qubit* qubit2, Classic alCondition & cbit, QCircuit(*oracle)(Qubit* qubit1, Qubit* qubit2)) {
auto prog = CreateEmptyQProg();
//Firstly, create a circuit container
prog << H(qubit1) << H(qubit2);
// Perform Hadamard gate on all qubits
prog << oracle(qubit1, qubit2);
// Finally, Hadamard the first qubit and measure it
prog << H(qubit1) << Measure(qubit1, cbit);
return prog;
}
QProg Two_Qubit_DJ_Algorithm_Circuit(Qubit * qubit1, Qubit * qubit2, ClassicalCondition & cbit, QGEN oracle) {
auto prog = CreateEmptyQProg();
//Firstly, create a circuit container
prog << H(qubit1) << H(qubit2);
// Perform Hadamard gate on all qubits
prog << oracle(qubit1, qubit2);
// Finally, Hadamard the first qubit and measure it
prog << H(qubit1) << Measure(qubit1, cbit);
return prog;
}
QProg DJ_Algorithm(QVec & qvec, ClassicalCondition & c) {
if (qvec.size() != 2){
QCERR("qvec size error£¬the size of qvec must be 2");
throw invalid_argument("qvec size error£¬the size of qvec must be 2");
}
bool fx0 = 0, fx1 = 0;
cout << "input the input function" << endl
<< "The function has a boolean input" << endl
<< "and has a boolean output" << endl
<< "f(0)= (0/1)?";
cin >> fx0;
cout << "f(1)=(0/1)?";
cin >> fx1;
std::vector<bool> oracle_function({ fx0,fx1 });
cout << "Programming the circuit..." << endl;
auto temp = Reset_Qubit(qvec[0], false);
temp << Reset_Qubit(qvec[1], true);
auto oracle = The_Two_Qubit_Oracle(oracle_function);
temp << Two_Qubit_DJ_Algorithm_Circuit(qvec[0], qvec[1], c, oracle);
return temp;
}
int main() {
init(QMachineType::CPU);
auto qvec = qAllocMany(2);
auto c = cAlloc();
auto prog = DJ_Algorithm(qvec, c);
directlyRun(prog);
if (c.eval() == false) {
cout << "Constant function!";
}
if (c.eval() == true) {
cout << "Balanced function!";
}
finalize();
}
整个文件利用 QPanda 的组件实现了一个 Deutsch-Jozsa 算法,并且提供了一个 2 Qubit 的示例。各个模块的介绍:
1. Deutsch_Jozsa_algorithm 函数
实现这个函数的时候,并不是仅仅考虑了 2 qubit 的情况,而是对更一般的情况,即所有 qubit 的情况进行处理。
QPanda 的核心逻辑在于对申请的量子比特进行量子线路构建, 因此,这个函数会返回一个 QProg 类型,这个 QProg 类型会被放到量子机器中进行执行。
Deutsch_Jozsa_algorithm 的参数有 4 个:
- vector
因此,这个算法的逻辑就可以表述为:通过输入的 qubit1, qubit2 构建量子线路; 并且将 oracle 作用在 qubit1 和 qubit2 上; 最后,对 qubit1 测量到 cbit 上。这个函数将量子算法的流程通过 QPanda 的组件编写出来,整个流程会被写入到一个 QProg 类型的对象中,最终,这个函数会返回这个对象。
auto prog = CreateEmptyQProg();
在函数中,首先可以通过 CreateEmptyQProg 函数去创建一个空的量子程序。
prog << X(qubit2);
prog << apply_QGate(qubit1, H) << H(qubit2);
将逻辑门插入到这个量子程序的后面,依次是 X 门作用在 qubit2 上(将 qubit2 初始化为|1⟩), 对 qubit1 和 qubit2 执行 Hadamard 门。
prog << oracle(qubit1, qubit2);
制备完纠缠态之后,就可以进行 oracle 计算。这里同样将 oracle 插入到量子程序中。
prog << apply_QGate(qubit1, H) << MeasureAll(qubit1, cbit);
最后同样是一组 Hadamard 门,并且通过 MeasureAll 将 qubit1 整个测量到 cbit 上。
2. two_qubit_deutsch_jozsa_algorithm 函数
这个函数对两个比特的情况提供了一个演示。在这种情况下,需要对不同情况构建oracle, 并且输入到这个算法中。
构建 oracle 的方式就是通过这个函数的参数——一个vector
std::vector<bool> fx = {0, 1};
这表示 fx[0] = 0, fx[1] = 1 这种情况。
通过真值表构建对应 oracle 的方法:即 generate_two_qubit_oracle,它恰好返回一个oracle 类型,感兴趣的读者可以自行对这个 oracle 中的不同情况进行验证。
这个函数中最重要的步骤就是初始化量子机器,申请量子比特和经典寄存器,取得量子程序,执行并且获得最终结果。
init(QMachineType::CPU);
这个语句初始化一个通过 CPU 执行的模拟器。 QMachineType 可以指定为不同类型,例如 GPU、 单线程 CPU、 或者云量子计算机。 通过抽象 QuantumMachine 保证操作它们的方式尽可能类似。
auto qvec = qAllocMany(2);
auto c = cAlloc();
通过 qAlloc 和 cAlloc 可以从量子机器中申请一定量的量子比特。 Many 表示很多,所以 qAllocMany 和 cAllocMany 可以一次性申请多个量子比特。
auto oracle = generate_two_qubit_oracle(boolean_function);
这个函数就是用于生成 oracle 的。
QProg prog;
prog << Deutsch_Jozsa_algorithm({ qvec[0] }, qvec[1], { c }, oracle);
通过前面申请到的 oracle, 量子比特和经典寄存器,再通过前面Deutsch_Jozsa_algorithm 算法函数,构建了待执行的量子程序 prog。
/* To Print The Circuit */
/*
extern QuantumMachine* global_quantum_machine;
cout << transformQProgToQRunes(prog, global_quantum_machine) <<endl;
*/
这一段程序可以将上述量子程序打印出来。
directlyRun(prog);
if (c.eval() == false) {
cout << "Constant function!" << endl;
}else if (c.eval() == true) {
cout << "Balanced function!" << endl;
}
函数 directlyRun 顾名思义是直接运行这个量子程序。 QPanda 提供很多运行量子程序的方式,而 directlyRun 表示这个量子程序在默认模式下运行 1 次。 由于 DJ 算法是一个确定性算法,就只运行一次, 运行结束后,可以从之前申请的经典寄存器中取得值:c.eval。 这里 false 表示测量到|0⟩, true 表示测量到|1⟩。 通过测量的结果可以得到这个函数属于平衡函数还是常数函数。
finalize();
finalize 是和 init 呼应的语句,它将所有运行的数据销毁。运行 finalize 之后还可以再次运行 init 函数去初始化, 但是之前申请的所有量子比特、经典寄存器,以及编写的量子程序与运行的结果会全部无效化。