量子计算学习 > 量子程序基础知识 > 量子线路与测量操作

量子线路与测量操作

量子线路是由代表量子比特演化的路线和作用在量子比特上的量子逻辑门组成的。量子线路产生的效果，等同于每一个量子逻辑门依次作用在量子比特上。在真实的量子计算机上，最后要对量子系统末态进行测量操作，才能得到末态的信息，因此也把测量操作作为量子线路的一部分，测量操作有时也称为测量门。测量背后的原理就是之前讲到的投影测量。

测量操作在线路上的显示如图 8.1：

图 2.2.9.1

图 8.1

它表示对该量子路线代表的量子比特进行测量操作。在计算基 $|0\rangle, |1\rangle$ 下，测量操作对应的矩阵形式为

$M_{0}=|0\rangle\langle0|=\begin{bmatrix} 1 & 0\\ 0 & 0 \end{bmatrix}$ $M_{1}=|1\rangle\langle1|=\begin{bmatrix} 0 & 0\\ 0 & 1 \end{bmatrix}$

如图 8.2 所示，是一个简单的单量子比特的量子线路。

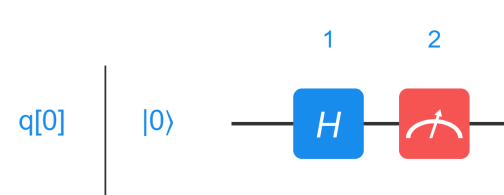
图 2.2.9.2

图 8.2

初始态为|0〉,首先经过一个 H 门，演化得到末态

$|\Psi ^{'}\rangle=H|0\rangle=\frac{\sqrt{2}}{2}\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} \begin{bmatrix} 1\\ 0 \end{bmatrix} =\frac{\sqrt{2}}{2}\begin{bmatrix} 1\\ 1 \end{bmatrix} = \frac{\sqrt{2}}{2}|0\rangle + \frac{\sqrt{2}}{2}|1\rangle$

接着就对其进行测量操作，得到投影到计算基 $|0\rangle$ 下的概率为

$p(0)=\langle\psi ^{'}|M_{0}^{\dagger}M_{0}|\psi ^{'}\rangle=\langle\psi ^{'}|M_{0}|\psi ^{'}\rangle=\begin{bmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{bmatrix} \begin{bmatrix} 1 & 0\\ 0 & 0 \end{bmatrix} \begin{bmatrix} \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \end{bmatrix} =\frac{1}{2}$

根据测量假设，测量过后末态 $|\psi ^{'}\rangle$ 变为新的量子态

$|\psi ^{''}\rangle=\frac{M_{0}|\psi ^{'}\rangle}{\sqrt{p(0)}}=\begin{bmatrix} 1\\ 0 \end{bmatrix} =|0\rangle$

投影到计算基 $|1\rangle$ 下的概率为

$p(1)=\langle\psi ^{'}|M_{1}^{\dagger}M_{1}|\psi ^{'}\rangle=\langle\psi ^{'}|M_{1}|\psi ^{'}\rangle=\begin{bmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{bmatrix} \begin{bmatrix} 0 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \end{bmatrix} =\frac{1}{2}$

根据测量假设，测量过后末态 $|\psi ^{'}\rangle$ 变为新的量子态

$|\psi ^{''}\rangle=\frac{M_{1}|\psi ^{'}\rangle}{\sqrt{p(1)}}=\begin{bmatrix} 0\\ 1 \end{bmatrix} =|1\rangle$

由于在真实的量子计算机上面，测量会对量子态有影响，所以只能够通过新制备初始量子态，让它重新演化，再进行测量，从而得到末量子态在计算基下的频率，用频率来近似概率，并且每次测量只能够用测量操作 $M_{0}$ 与 $M_{1}$ 中的一个进行测量。

图 8.3，表示的是两量子比特的量子线路

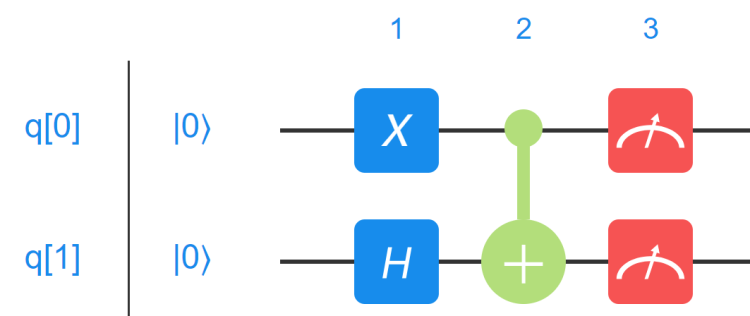
图 2.2.9.3

图 8.3

在该量子线路中，初始态 q[1]、q[0]代表量子比特的初始态均为|0〉，因此该系统的复合量子态为|00〉，这里复合量子态|00〉的从左到右依次对应高位比特到低位比特。首先该复合的量子比特在时刻 1 同时经过 H 门和 X 门，接着在时刻 2 经过 CNOT 门，最后在时刻 3 进行整体测量操作。下面用数学的语言进行描述，在初始时刻系统处在初始态 $|\psi_{0}\rangle=|00\rangle$ ，其中左边的 0 为高位 q[1],右边的 0 为低位 q[0]，经过时刻 1 的门以后量子态变为

$|\psi_{1}\rangle=[H\bigotimes X]|00\rangle=\frac{\sqrt{2}}{2}\begin{bmatrix} X & X\\ X & -X \end{bmatrix} = \frac{\sqrt{2}}{2}\begin{bmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 \end{bmatrix} \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} = \frac{\sqrt{2}}{2} \begin{bmatrix} 0\\ 1\\ 0\\ 1 \end{bmatrix}$

接着在时刻 2 经历 CNOT 门后，演化为

$|\psi_{2}\rangle=CNOT|\psi_{1}\rangle = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0\\ \frac{\sqrt{2}}{2}\\ 0\\ \frac{\sqrt{2}}{2} \end{bmatrix} = \begin{bmatrix} 0\\ \frac{\sqrt{2}}{2}\\ 0\\ \frac{\sqrt{2}}{2} \end{bmatrix} = \frac{\sqrt{2}}{2}|01\rangle+\frac{\sqrt{2}}{2}|11\rangle$

最后，到时刻 3 进行测量操作，若用测量操作 $M_{00}=|00\rangle\langle00|$ ，则得到投影到计算基 $|00\rangle$ 下的概率为

$p(00)=\langle\psi_{2}|M_{00}^{\dagger}M_{00}|\psi_{2}\rangle=\langle\psi_{2}|M_{00}|\psi_{2}\rangle=\langle\psi_{2}|[|00\rangle\langle00|]|\psi_{2}\rangle=\begin{bmatrix} 0 & \frac{\sqrt{2}}{2} & 0 & \frac{\sqrt{2}}{2} \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0\\ \frac{\sqrt{2}}{2}\\ 0\\ \frac{\sqrt{2}}{2} \end{bmatrix}=0$

根据测量假设，由于 $p(00)=0$ ，因此测量过后，量子态 $|\psi_{2}\rangle$ 不可能坍缩在基态 $|00\rangle$ 上面。

若用测量操作 $M_{01}=|01\rangle\langle01|$ ，则得到投影到计算基 $|01\rangle$ 下的概率为

$p(01)=\langle\psi_{2}|M_{01}^{\dagger}M_{01}|\psi_{2}\rangle=\langle\psi_{2}|M_{01}|\psi_{2}\rangle=\frac{1}{2}$

对量子态 $|\psi_{2}\rangle$ 测量后，得到新的量子态为

$|\psi_{3}\rangle=\frac{M_{01}|\psi_{2}\rangle}{\sqrt{p(01)}}=\begin{bmatrix} 0\\ 1\\ 0\\ 0 \end{bmatrix}=|01\rangle$

若用测量操作 $M_{10}=|10\rangle\langle10|$ ，则得到投影到计算基 $|10\rangle$ 下的概率为

$p(10)=\langle\psi_{2}|M_{10}^{\dagger}M_{10}|\psi_{2}\rangle=\langle\psi_{2}|M_{10}|\psi_{2}\rangle=0$

所以测量过后，量子态 $|\psi_{2}\rangle$ 不可能坍缩在基态 $|10\rangle$ 上面。

若用测量操作 $M_{11}=|11\rangle\langle11|$ ，则得到投影到计算基 $|11\rangle$ 下的概率为

$p(11)=\langle\psi_{2}|M_{11}^{\dagger}M_{11}|\psi_{2}\rangle=\langle\psi_{2}|M_{11}|\psi_{2}\rangle=\frac{1}{2}$

对量子态 $|\psi_{2}\rangle$ 测量后，得到新的量子态为

$|\psi_{3}\rangle=\frac{M_{11}|\psi_{2}\rangle}{\sqrt{p(11)}}=\begin{bmatrix} 0\\ 0\\ 0\\ 1 \end{bmatrix}=|11\rangle$

有时可能关心线路中某些位量子比特的演化结果，那么就把测量放在某些量子对应的路线上面。如图 8.4 所示，将测量操作放在高位比特所对应路线上面。

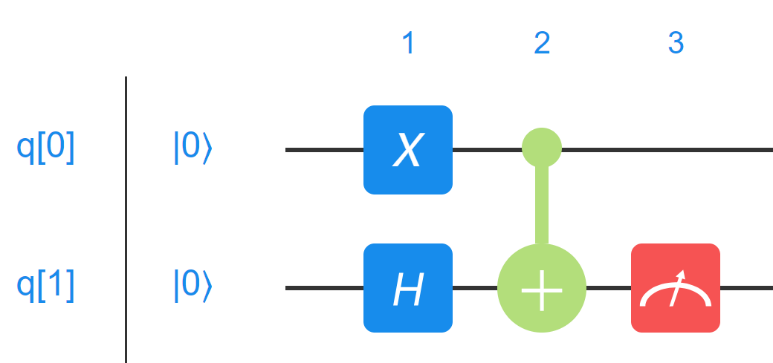
图 2.2.9.4

图 8.4

此时测量对应的矩阵形式为

$M_{0}^{1}=\sum_{i\in \{0,1\}}|0i\rangle\langle0i|$ 和 $M_{1}^{1}=\sum_{i\in \{0,1\}}|1i\rangle\langle1i|$

因此通过测量得到测量结果 0 和 1 发生的概率分别为

$p_{1}(0)=\langle\psi_{2}|M_{1}^{0}|\psi_{2}\rangle = \begin{bmatrix} 0 & \frac{\sqrt{2}}{2} & 0 & \frac{\sqrt{2}}{2} \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0\\ \frac{\sqrt{2}}{2}\\ 0\\ \frac{\sqrt{2}}{2} \end{bmatrix}= \frac{1}{2}$

$p_{1}(1)=\langle\psi_{2}|M_{1}^{1}|\psi_{2}\rangle = \begin{bmatrix} 0 & \frac{\sqrt{2}}{2} & 0 & \frac{\sqrt{2}}{2} \end{bmatrix}\begin{bmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0\\ \frac{\sqrt{2}}{2}\\ 0\\ \frac{\sqrt{2}}{2} \end{bmatrix}= \frac{1}{2}$

测量后，量子系统的状态分别变为

$|\psi_{3}\rangle=\frac{M_{1}^{0}|\psi_{2}\rangle}{\sqrt{p_{1}(0)}}=|01\rangle$ $|\psi_{3}\rangle=\frac{M_{1}^{1}|\psi_{2}\rangle}{\sqrt{p_{1}(1)}}=|11\rangle$

同理，对低位比特 q[0]进行单独测量时,线路图如图 8.5 所示：

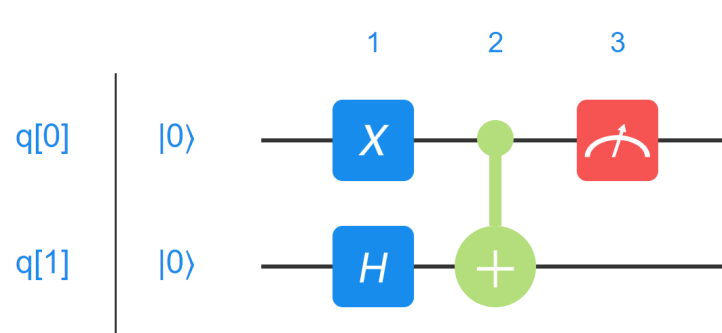
图 2.2.9.5

图 8.5

此时测量操作对应的矩阵形式为

$M_{0}^{0}=\sum_{i\in \{0,1\}}|0i\rangle\langle0i|$ 和 $M_{1}^{0}=\sum_{i\in \{0,1\}}|1i\rangle\langle1i|$

通过测量，得到测量结果 0 发生的概

$p_{0}(0)=\langle\psi_{2}|M_{0}^{0}|\psi_{2}\rangle = \begin{bmatrix} 0 & \frac{\sqrt{2}}{2} & 0 & \frac{\sqrt{2}}{2} \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0\\ \frac{\sqrt{2}}{2}\\ 0\\ \frac{\sqrt{2}}{2} \end{bmatrix}= 0$

得到测量结果 1 发生的概率为

$p_{0}(1)=\langle\psi_{2}|M_{0}^{1}|\psi_{2}\rangle = \begin{bmatrix} 0 & \frac{\sqrt{2}}{2} & 0 & \frac{\sqrt{2}}{2} \end{bmatrix}\begin{bmatrix} 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0\\ \frac{\sqrt{2}}{2}\\ 0\\ \frac{\sqrt{2}}{2} \end{bmatrix}= 1$

测量后系统由原来的量 $|\psi_{2}\rangle$ 演化为量子状态

$|\psi_{3}\rangle=\frac{M_{0}^{1}|\psi_{2}\rangle}{\sqrt{p_{0}(1)}}=\frac{\sqrt{2}}{2}|01\rangle+\frac{\sqrt{2}}{2}|11\rangle$