量子计算学习 > 量子程序基础知识 > 多量子比特逻辑门

多量子比特逻辑门

不论是在经典计算还是量子计算中，两量子比特门无疑是建立量子比特之间联系的最重要桥梁。不同于经典计算中的与或非门及它们的组合，量子逻辑门要求所有的逻辑操作必须是酉变换，所以输入和输出的比特数量是相等的。

在描述两量子比特门之前，必须要将之前对于单量子比特的表示方式扩展一下。联立两个量子比特或者两个以上的量子比特时，就用到复合系统中量子态演化的假设。

对于一个 n 量子比特 $|x_{n-1}\cdots x_{0}\rangle$ ，n 量子比特系统的计算基就有 $2^{n}$ 单位正交矢量组成，借助于经典比特的进位方式对量子比特进行标记，从左到右依次是二进制中的从高位到低位，也就是说 $|x_{n-1}\cdots x_{0}\rangle$ 中 $x_{n-1}$ 为高位， $x_{0}$ 为低位。

比如对于一个 2 量子比特的系统，其计算基分别记做

$|00\rangle=\begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} , |01\rangle=\begin{bmatrix} 0\\ 1\\ 0\\ 0 \end{bmatrix}$

$|10\rangle=\begin{bmatrix} 0\\ 0\\ 1\\ 0 \end{bmatrix} , |11\rangle=\begin{bmatrix} 0\\ 0\\ 0\\ 1 \end{bmatrix}$

在基态 $|01\rangle$ 中，左侧的 0 对应的位为高位，右侧的 1 对应的位为低位。

在介绍 2 比特量子逻辑门时，会使用如图 7.1 的图标：

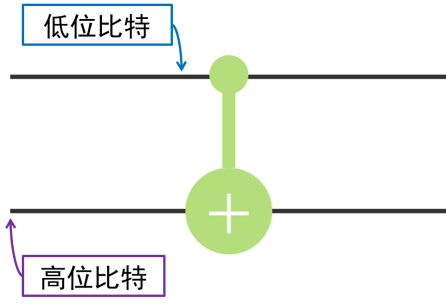
图 2.2.8.1

图 7.1

每根线表示一个量子比特演化的路线，这和单比特门中的横线是类似的，不一样的是这两根线有位次之分，从上到下依次分别表示从低位到高位的量子比特演化的路线。这个图标横跨两个量子比特，它代表将一个两比特门作用在这两个量子比特上，这个图标代表的是 CNOT 门。

7.1 CNOT

控制非门(Control-NOT)，通常用 CNOT 进行表示，是一种普遍使用的两量子比特门。若低位为控制比特，那么它具有如下的矩阵形式:

$CNOT=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 \end{bmatrix}$

对应的 CNOT 门在线路中显示如图 7.2：

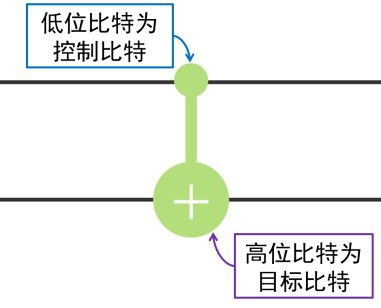
图 2.2.8.2

图 7.2

含实点的路线对应的量子比特称为控制比特（control qubit），含+号的路线对应的量子比特为目标比特（target qubit）。

假设，CNOT 门作用分别作用在基态|ψ〉 = |00〉、|01〉、|10〉、|11〉上面, 得到新的量子态为：

$|\psi ^{'}\rangle=CNOT|00\rangle =\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} = \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} = |00\rangle$ $|\psi ^{'}\rangle=CNOT|01\rangle =\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0\\ 1\\ 0\\ 0 \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ 0\\ 1 \end{bmatrix} = |11\rangle$ $|\psi ^{'}\rangle=CNOT|10\rangle =\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0\\ 0\\ 1\\ 0 \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ 1\\ 0 \end{bmatrix} = |10\rangle$ $|\psi ^{'}\rangle=CNOT|11\rangle =\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0\\ 0\\ 0\\ 1 \end{bmatrix} = \begin{bmatrix} 0\\ 1\\ 0\\ 0 \end{bmatrix} = |01\rangle$

由于右侧的低位比特为控制比特，左侧的高位比特为目标比特，所以当右侧的低位比特位置对应为 1 时，左侧的高位比特就会被取反；当右侧的低位比特位置为 0 时，不对左侧的高位比特做任何操作。

若左侧的高位比特为控制比特，那么它具有如下的矩阵形式:

$CNOT =\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{bmatrix}$

CNOT 门在线路中显示如图 7.3：

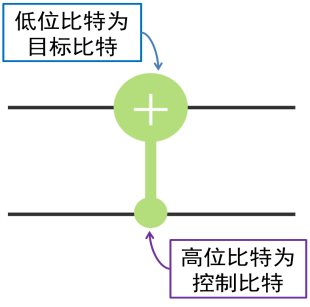
图 2.2.8.3

图 7.3

假设，高位为控制比特，CNOT 门分别作用在基态|ψ〉 = |00〉、|01〉、|10〉、|11〉上，那么，可以计算四个两量子比特的计算基经 CNOT 门的演化结果如图 7.4 所示：

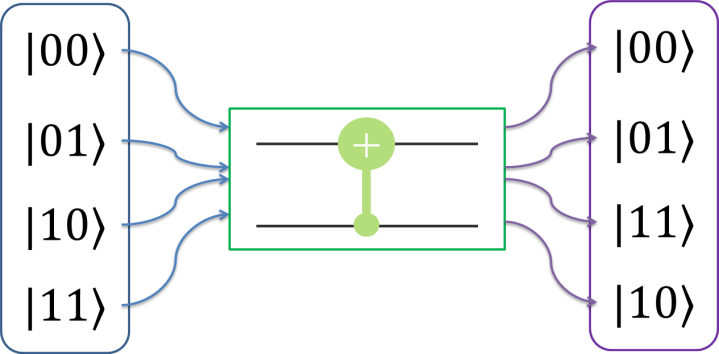
图 2.2.8.4

图 7.4

从上例可以看出 CNOT 门的含义是当控制比特为|0⟩态时，目标比特不发生改变；当控制比特为|1⟩态时，对目标比特执行 X 门(量子非门)操作。要注意的是控制比特和目标比特的地位是不能交换的。

7.2 CR 门

控制相位门（Controlled phase gate）和控制非门类似，通常记为 CR(CPhase)，其矩阵形式如下

$CR(\theta) =\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & e^{i\theta} \end{bmatrix}$

CPhase 门在线路中显示如图 7.5：

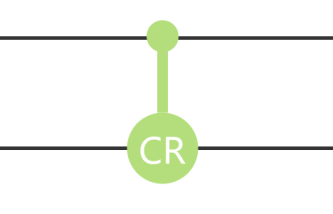
图 2.2.8.5

图 7.5

在 CPhase 门的图标中，含实点的路线对应的量子比特称为控制比特（control qubit），含 CR 字母的路线对应的量子比特为目标比特（target qubit）。

当控制比特为|0⟩态时，目标比特不发生改变；当控制比特为|1⟩态时，对目标比特执行相转变门（phase-shift gate），其特殊的是，控制相位门里交换控制比特和目标比特的角色，矩阵形式不会发生任何改变。

7.3 iSWAP 门

iSWAP 门的主要作用是交换两个比特的状态，并且赋予其 $\frac{\pi}{2}$ 相位；经典电路中也有 SWAP 门，但是 iSWAP 是量子计算中特有的。iSWAP 门在某些体系中是较容易实现的两比特逻辑门，它是由 $\sigma _{x} \bigotimes \sigma _{x} + \sigma _{y} \bigotimes \sigma _{y}$ 作为生成元生成，需要将矩阵 $\sigma _{x} \bigotimes \sigma _{x} + \sigma _{y} \bigotimes \sigma _{y}$ 对角化，iSWAP 门的矩阵表示如下：

$iSWAP(\theta) =\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & cos(\theta) & -isin(\theta) & 0\\ 0 & -isin(\theta) & cos(\theta) & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$

iSWAP 门在线路中显示如图 7.6：

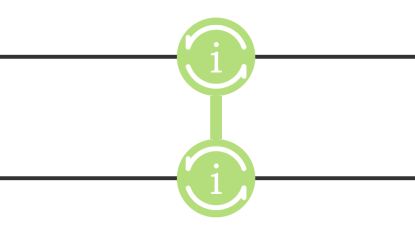
图 2.2.8.6

图 7.6

通常会用一个完整的翻转，即 $\theta = \frac{\pi}{2}$ 的情况来指代 iSWAP。当角度为 iSWAP 的一半时，即 $\theta = \frac{\pi}{4}$ ，称之为 $\sqrt{iSWAP}$ 。对于 iSWAP 门而言，两个比特之间地位是对等的，不存在控制和受控的关系。