两能级系统 Two Level System
事物的二元化:0和1、无和有、高和低、开和关、天和地、阴和阳、生和死、产生和消灭。二元化是一种将事物关系简化的哲学,基于二进制的计算理论正是利用了这种哲学思想。
在谈论量子计算原理前,先了解经典计算机的工作流程。经典计算机就是在不断地处理0、1的二进制数码,它们代表着逻辑电路中的高低电平,对于这些二进制数码的产生、传输、处理、读取,最终反馈到像显示器这种输出设备上的信号,就是一个计算机的工作流程。
对于微观量子而言,有一个决定粒子性质的最直接参量——能量。粒子的能量只会在几个分立的能级上面取值,限制取值的可能性种类为两种,这就构成了两能级系统。
除了某些特殊的情况之外,这两个能级必定能找出来一个较低的,称之为基态(ground state),记为
;
另一个能量较高的,称之为激发态(excited state),记为
。
量子计算机里面也由两种状态来构成基本计算单元,只不过这里的两种状态是指量子态的
和
这就是一个两能级系统的特征。以列矢量的方式将它们记为
行矢量的形式记为
和经典的比特类比,常将|e⟩记做|0⟩,将|g⟩记做|1⟩,并称之为量子比特(quantum bits)。
任意叠加态(superposition) 可以写作|0⟩和 |1⟩的线性组合
好吧,我敢肯定有的同学读到这里肯定忘了啥叫任意叠加态,你可以快速跳转到量子叠加性去补习一下。
如果你还不明白,那么我们又要祭出那只可怜的小猫咪了
其中复数 α 和 β 称为振幅(amplitudes),并且满足归一化条件。
其中 |α| 表示复数 α 的模。
我估计读到这里,很多同学又懵圈,不要骗自己,你真的懂啥是振幅么?什么是归一化?为啥满足归一化条件?如果你不理解,我很推荐你读一下这篇文章波函数的形式:希尔伯特空间中的骰子
好吧,我承认作者写的太长了,那么让我们利用之前讲过的知识,来说明一下。我们曾在状态的演化里面提到过,“量子态可以想象成一个单位球面上的点”。 那么就可以表示成下面这个图的样子。
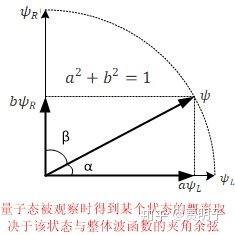
有了勾股定理的加持,是不是理解起来轻松多了,为啥这个圆的半径一定是1呢?其实这里代表的应该是100%,简化成1,也就是说,该半圆半径代表所有的可能性的概率的和。 这个很好理解,因为一个量子态是确定的,不存在概率性,它的总的概率必须是1。那么我们来看这个总的波函数的两个分量,左缝波和右缝波的分量分别算作三角形的两个直角边,那么叠加的波函数就是它的斜边。