量子计算学习 > 量子力学基础理论 > 密度矩阵和布洛赫球 Density Matrix And Bloch Sphere

密度矩阵和布洛赫球 Density Matrix And Bloch Sphere

态矢是对纯态的描述，如果要描述一个混合态，就必须写成态集合和概率的列表形式，非常繁琐。因此采用密度矩阵来描述。

对于一个纯态而言，密度矩阵的形式是：

$\rho = |\psi\rangle \langle \psi|$

而对于一个混合态而言，密度矩阵的形式

$\rho = \sum_{i}p_{i}|\psi _{i}\rangle\langle\psi _{i}|$

其中 $\left \{ p_{i}, |\psi _{i}\rangle \right \}$ 是系统所处的态及其概率。

密度矩阵有以下的性质:

对于一个两能级体系表述的态，不论是纯的还是混合的，都可以用密度矩阵 $\rho$ 表示。
当且仅当量子态时纯态时 $\rho = \rho ^{2}$ 成立。
$\rho$ 对角线上的分量表示整个系统如果经历一次测量，那么可以得到这个态的概率。如果只去操作和测量一个两能级体系，那么是分辨不出相同的密度矩阵的。
密度矩阵已经完备地表示了一个两能级系统可能出现的任何状态。为了更加直观地理解量子叠加态与逻辑门的作用，引入布洛赫球的概念，如图 2.1.12.1，它能够方便地表示一个量子比特的任意状态。

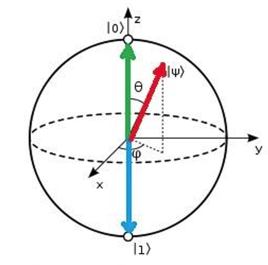
图 2.1.12.1

如果量子态是一个纯态，那么它是球面上的点。点的z坐标衡量了它的 |0⟩ 和 |1⟩ 的概率，即

$p(0) = \frac{1 + z}{2}$

$p(1) = \frac{1 - z}{2}$

最上面表示 |0⟩ 态，最下面表示 |1⟩ 态。

再沿着平行于 XY 平面的方向，并且穿过这个点的 Z 坐标，可以得到一个圆，这个圆就象征着相位的复平面；这个点在这个圆上交 X 轴的角度就是单位复数的幅角。经过这个过程可以将每个纯态都与球面上的点一一对应了起来。

对于混合态而言，因为根据之前的描述，混合态实际上是多个纯态的经典统计概率的叠加。对于每一个纯态分量，连接球心和球面上的点，可以形成一个矢量。根据概率列表，对所有的纯态矢量进行加权平均，即可得到混合态的矢量，即得到了混合态对应的点。

混合态是布洛赫球内部的点，根据混合的程度不同，矢量的长度也不同。最大混合态是球心，它意味着这里不存在任何量子叠加性。

例如(1,0,0)和(-1,0,0)点在布洛赫球上就是在 X 方向上的顶点和-X 方向上的顶点。它们对应的量子态的概率分布就是 Z 坐标，即为 0。所以，

$p_{0}(|\psi _{1}\rangle)=p_{0}(|\psi _{2}\rangle)=0.5$

沿 XY 平面横切，得到一个圆，可以看到这两个点对应的幅角是 $\theta _{1} = 0, \theta _{2} = \pi$ ，由此推断出量子态分别为:

$|\psi _{1}\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$

$|\psi _{2}\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)$

如果将这两个态以 $\frac{1}{2}$ 和 $\frac{1}{2}$ 的概率混合，在布洛赫球上面的坐标将表示为(0,0,0)，也就是球心。对应到密度矩阵的表述，为：

$\rho =\frac{1}{2}|\psi _{1}\rangle\langle\psi _{1}|+\frac{1}{2}|\psi _{2}\rangle\langle\psi _{2}|=\begin{bmatrix} 0.5 & 0\\ 0 & 0.5 \end{bmatrix}$

即为最大混合态。